一个聪明的量子戏法——相位反冲，告诉你如何进行量子计算量子计算充满了技巧

文章图片

文章图片
【一个聪明的量子戏法——相位反冲，告诉你如何进行量子计算】量子计算充满了技巧，可以帮助我们解决那些用经典计算需要花费数年才能解决的问题。这些技巧通常涉及一个相对较小的电路，在一个大得多的算法中执行一个特定任务。你可能已经听说过其中的一些技巧，比如纠缠和叠加。还有很多，其中非常重要的一个便是相位反冲。
相位反冲是一个非常常见和有用的技巧，你会经常看到它包含在较大的量子算法中。这就是为什么理解它很重要，它将帮助你直观地理解其他更实用的电路，并对引擎盖下发生的事情有一个概念，而不仅仅是看大体的想法。
我们将看一个非常简单的例子，只涉及两个量子比特。为了使这一技巧发挥作用，我们需要考虑的一个重要要求是，在控制操作中作为目标的量子位，在我们的例子中是量子比特q1 ，需要是这个运算的特征向量。
我们想通过这个要求实现的是，对我们的目标量子位施加运算并不改变其状态，而只是影响其相位。因此，在我们的量子比特上应用运算符会看起来像这样。

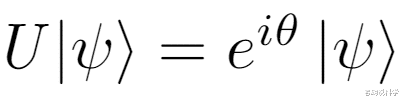
文章图片

文章图片
在这个例子中， U是作用于量子比特psi（用ket表示的矢量）的运算（一个矩阵）。正如你所看到的，这个运算只是给量子比特增加了一个相位，但并没有改变它的状态。
有了这个要求，我们就可以了解电路了。首先，让我们看看这个电路是什么样子的，接下来我们将了解每个门的作用。

文章图片

文章图片
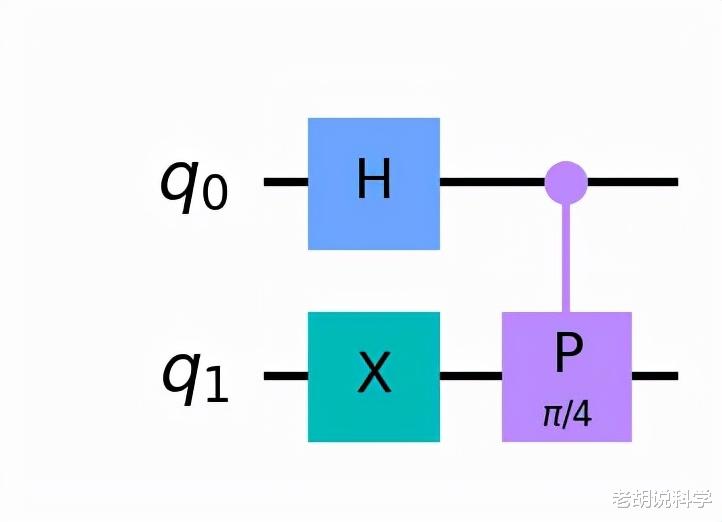
基本的相位反冲量子电路
首先，顶部量子比特通过哈达玛门（Hadamard gate），底部量子比特通过保利-X门（Pauli-X gate），具有以下状态：

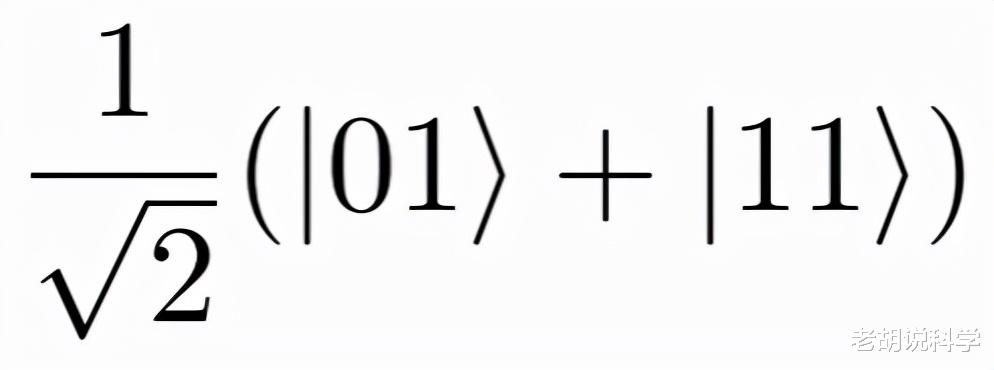
文章图片

文章图片
第一个方程，显示了状态01和11之间的等量叠加
我们可以看到，我们有一个状态01和11的等量叠加，其中第一个数字对应于量子比特q0 ，第二个数字对应于量子比特11 。这种状态的产生是因为哈达玛门将顶部量子比特放入状态0和1之间的等量叠加，而Pauli-X门无论如何都要将底部量子比特放入状态1 。
这时就变得有趣了。这些量子比特通过一个受控的相位门，其中控制量子比特是顶部的，目标量子比特是底部的。在这种情况下，控制和目标这两个名字有误导性，因为最终改变其相位的量子比特是控制量子比特。请记住，受控门只在控制量子比特处于状态1时发挥作用，所以相位旋转只适用于这种情况。当通过这个门时，产生的状态如下。

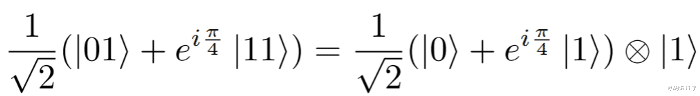
文章图片

文章图片
第二个方程，证明了在第一个量子位中的相对相位
还记得我们之前谈到的要求吗？那么，你可以在这里看到它的作用。相位门被应用于状态11（因为作为控制的顶部量子比特处于状态1），但它只是给状态增加了一个相位。在这种情况下， θ=π/4 ，遵循我们上面的公式。另一个重要的说明是，这些状态不是纠缠的，因为我们可以把它们写成两个量子比特的张量积。