解释粒子具有质量的最佳机制—自发对称性破缺，如何理解负质量？物理学在很多方面都是关于对

文章图片

文章图片
物理学在很多方面都是关于对称性的。正如我在以前的文章中多次提到的，一个物理系统的对称性决定了它的许多属性。这些属性之一是一个系统所具有的守恒量。例如，如果一个物理系统具有旋转对称性，那么其物体的旋转动量是守恒的。同样，如果一个系统具有平移对称性，那么在一条直线上运动的物体的动量也是守恒的。
到目前为止，守恒量还不是现代物理学中对称性的唯一用途。我了解到的一个令人惊讶的概念是对称性在创造粒子本身中的作用。这个过程被称为自发对称性破缺（spontaneous symmetry breaking），它是描述粒子为什么有质量的最佳机制。在我详细介绍之前，我先简单地解释一下：在低能量下，一个系统可能会从一个对称状态突破到一个非对称状态。当这种情况发生时，我们会发现奇怪的、短暂的粒子突然出现，虽然这种机制被用于研究高能理论物理学，但它也广泛适用于像磁铁这样熟悉的东西。
朗道-金兹堡模型?（The Landau-Ginzburg Model）
一个物理系统通常用一个拉格朗日量（函数）来描述，即系统的动能和势能之和。例如，如果势能看起来是圆柱形或漏斗形，那么拉格朗日量可能拥有旋转对称性，因为旋转它不会产生任何影响。另一方面，如果我们看一个有大量能量的系统，拉格朗日量的对称性往往被保留下来。
为了解释这一点，我们将研究一种控制磁性材料中原子集合的机制。这一机制最初是由物理学家金兹堡和朗道提出的。首先，他们为磁性材料定义了一个拉格朗日量，旨在捕捉其关键特征。拉格朗日量是对物理系统的信息进行紧凑编码的一种方法，通常是根据系统的对称性进行猜测。拉格朗日公式是这样提出的。我也写了一个定性的版本，使它更容易阅读。

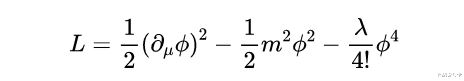
文章图片

文章图片
由于他们想描述许多不同粒子的集体行为，拉格朗日量不只是代表一个单一的粒子，而是一个场。场在上面的表达中用希腊字母phi表示。场指的是在空间的每一点都有属性的物理对象，比如房间里的温度。拉格朗日量中的第一个项描述了场本身的动能。他们还包括一个类似于某种 "质量 "属性的术语。这就是拉格朗日量的第二个项。最后一个项旨在描述粒子之间的相互作用，这些粒子之间的相互作用强度用数字λ（lambda）来表示。
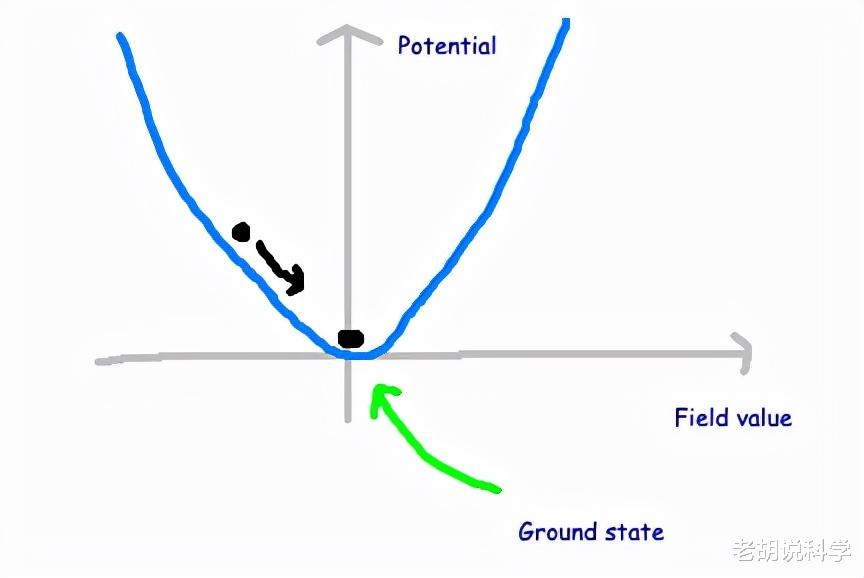
当场具有正质量时，拉格朗日量看起来就像下图中的势阱（potential well），在这种情况下，场的"稳定状态 "位于这个势阱的底部。物理学家把这称为基态（ground state）。在正质量的情况下，基态发生在场值等于零的地方。在这样的物理问题中，我们所做的一切几乎都与基态有关。

文章图片

文章图片
当变冷时会发生什么？?
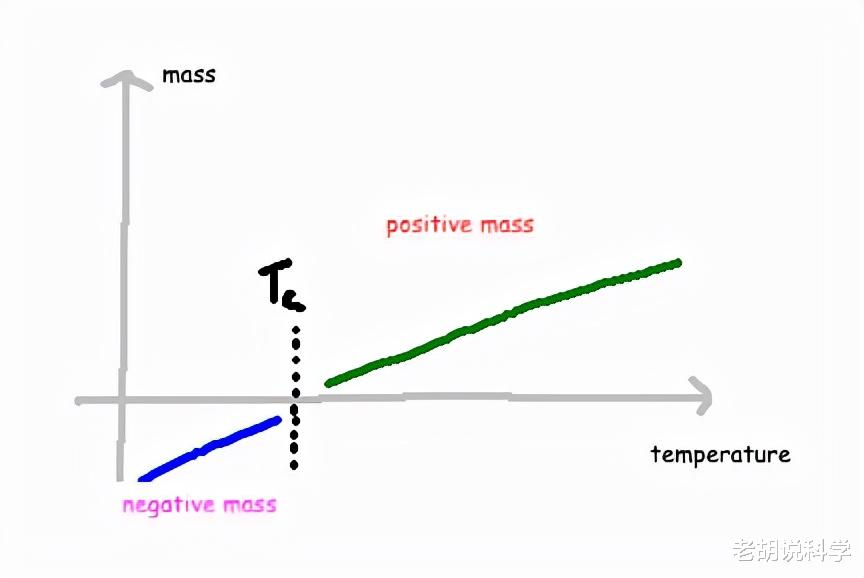
朗道和金兹堡随后提出了一些迷人的问题，从这个拉格朗日量中得到一些令人兴奋的物理学。例如，当我们降低系统的温度时会发生什么？由于在这个拉格朗日量中没有明确的温度项，我们如何能将其纳入其中呢？第一个猜测是尝试使质量取决于温度。所以他们创建了一个模型，根据温度是否足够冷，质量突然变成负数。