量子理论与相对论格格不入，有一点却又是如此的默契( 二 ) 本文原创作者：水木长龙在经

文章图片

文章图片
第二，非正交量子态的不可区分是阻挠“超光速通信”的第二道门槛。
“非正交量子态”是什么？该如何理解呢？不如我们这样理解：我们知道处于纠缠态的两个正负电子，当测知其中一个为左旋时，必然得知另一个为右旋。这是根据处于纠缠态中两电子的“旋转纠缠特性”来获知在测量到一个电子的旋转状态时便可立即判断出另一电子的波函数坍缩后会是什么旋转状态的方法。但是，第一道门槛时我们说了，单个未知量子态具有不可全测的阻挠。假如处于纠缠态的一对量子，在形成的纠缠系统中旋转状态并不正交——当测知一个向左，另一个必然会向右——而是都向左，或者都向右，也就是说纠缠的本征特性不再以“旋转正交”为判断依据，而是以某种我们不知道的未知特征为依据，这时以我们的“不可知”如何去实现“超光速信息”的获取呢？所以，非正交量子态的不可区分是阻挠“超光速通信”的第二道门槛。

文章图片

文章图片
第三，测量所导致的随机坍缩是阻挠“超光速通信”的第三道门槛。
在量子力学里，对于处于纠缠系统中的量子而言，在未进行测量之前——即波函数坍缩之前，每一个纠缠中的量子都处于各种可能性的叠加态。只有在进行测量的时候，随着波函数的坍缩，被测量的量子才会呈现出具体的状态。如果知道该纠缠系统的“本征纠缠特性” ，那么便可以根据测量的量子瞬间超光速地获知另一处于纠缠态中的量子状态，因为测量在导致被测量子波函数坍缩的时候，会超距瞬间影响到另一量子的波函数同时出现坍缩过程。但是，对于纠缠中的两个量子，如果“本征纠缠特性”不是正交的两个，而是具有多种可能状态值，比如：如果量子1被测是A+B状态，那么可以得知量子2是C、D或者C+D状态中的某一种状态；当测得量子1为B+D状态时，可以得知量子2的状态为A、C或A+C状态中的某一种。但是，无论测得量子1的确切状态如何，只能在其波函数坍缩的时候，得知量子2处于三种可能坍缩结果中的其中一种，而无法确切地知道量子2究竟是哪一种坍缩结果。这就是测量所导致的随机坍缩是阻挠“超光速通信”的第三道门槛。

文章图片

文章图片
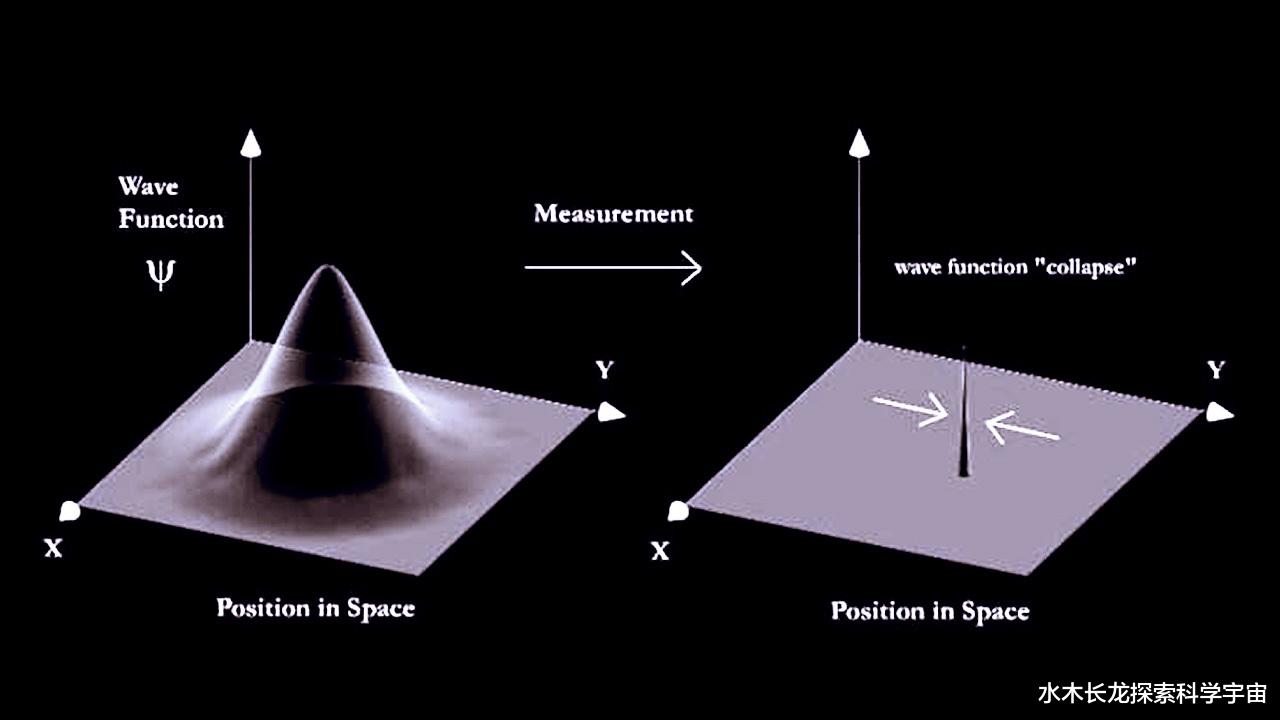
第四，贝尔定理的非定域关联测量是阻挠“超光速通信”的第四道门槛。
如果对于“多量子纠缠”——超过两个纠缠量子——系统中的量子进行测量，测量需要进行多次，才能最终确定每一个量子波函数坍缩后的最终确定结果。而这需要花费更多的时间，仅“测量”就已经阻断了超光速的可能性。所以，贝尔定理的非定域关联测量是阻挠“超光速通信”的第四道门槛。
第五，纠缠态的一次性坍缩是阻挠“超光速通信”的第五道门槛。
其实，水木认为这第五条才是最为关键，甚至应该作为前四条之首——第一道门槛才对。之所以放到第五，量子学界还存有诸多争议。此处，水木这样解释：对处于纠缠态中的两个量子，当对其中一个量子进行了测量，在导致该量子的波函数发生坍缩时，另一个纠缠态的量子波函数也会同时发生坍缩，从而两个纠缠态的量子就会在测量下分别但同时坍缩为确定的状态，一旦状态确定，也就解开了彼此的纠缠关系，而变成了独立存在状态——之后，无论再怎么对这曾经处于纠缠态的两个量子进行测量，都不会再发生状态的改变，因为纠缠态已经被测量解除了关联。既然如此， “量子超距通信”又怎么可能实现？尤其加密就更不可能了。