万有引力定律：牛顿在《自然哲学》中所发表( 二 ) 到底是什么样的公式

4、万有引力定律
英文：
LawofGravity
公式：

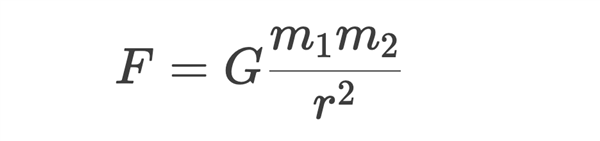
文章图片

文章图片

定义：
任何两个质点都存在通过其连心线方向上的相互吸引的力：
该引力大小与它们质量的乘积成正比与它们距离的平方成反比，与两物体的化学组成和其间介质种类无关。
其中， F表示两个物体之间的引力；G表示万有引力常量；m1和m2分别表示物体1和物体2的质量；r则是两个物体之间的距离（大小）。
万有引力定律是牛顿于1687年在《自然哲学的数学原理》上所发表，可以说是17世纪自然科学最伟大的成果之一。
他用万有引力定律证明了开普勒定律、月球绕地球的运动、潮汐的成因和地球两极较扁等自然现象。
因此，牛顿的万有引力定律是天体力学的基础。人造卫星、月球和行星探测器的轨道，都是以这个定律为基础来计算的。
5、-1的平方根
英文：
Thesquarerootof-1
公式：

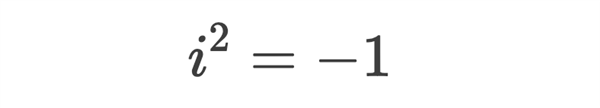
文章图片

文章图片

数学家们一直在对数字的概念做着拓展工作，例如从自然数到负数、分数，再到实数。
而在16世纪，意大利米兰学者卡当首次引入了复数的概念。
经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，这个概念逐渐被数学家接受。
从数学角度来看，复数可以说是极其优雅，任何方程都有一个复数解，但这种情况在实数却不成立。
例如，对于x2+4=0 ，就是没有实数解的，而放眼复数，解就是-4或2i 。
而微积分也是可以拓展到复数，数学家们由此还发现了一些数所具备的对称性和性质。
这些特性便使得复数在电子学和信号处理中起到了重要的作用。
6、多面体欧拉定理
英文：
Euler’sPolyhedraFormula
公式：

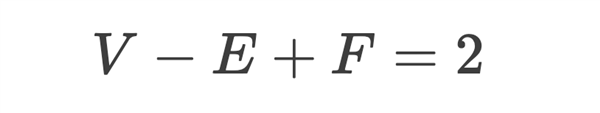
文章图片

文章图片

定义：
对于n维空间中的简单多面体，其零维对象数（即顶点数）D0、一维对象数（即边数）D1、二维对象数（即面数）D2、三维对象数（即体数）D3、……、n维对象数Dn：

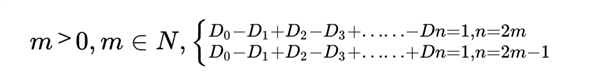
文章图片

文章图片

其中符号为正负号交替出现，等式一边是各维对象数的重复加减，等式另一边是1 。
一般以V（Vertex）表示零维对象（即顶点）数D0 ，以E（Edge）表示一维对象（即边、棱）数D1 ，以F（Flatsurface）表示二维对象（即面）数D2 ，以S（Solid）表示三维对象（即体）数D3 ，以P表示四维对象数D4 。
对于一般的三维空间，该公式表达为：V–E+F–S=1 。
由于对于一个三维物体，其体数S总是1 ，因此就得到上述的那个公式。
欧拉的这项观察，现在被视为拓扑不变性的最早的例子之一。
连同他对柯尼斯堡桥问题的解决，可以说是为拓扑学的发展铺平了道路，使其成为现代物理学必不可少的一个数学分支。
……
由于篇幅原因，其它公式便不一一展开，感兴趣的友友们可以访问文末链接查看详情。
马斯克pick了哪个公式？
最后，揭晓开头的答案。
马斯克喜欢的公式是：

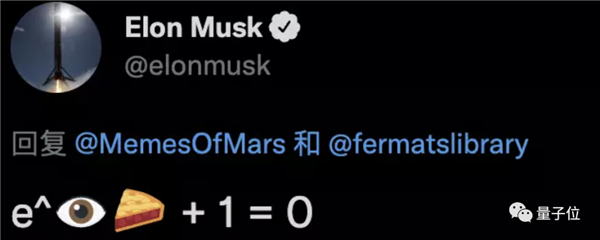
文章图片

文章图片