光竟然有压力？《张朝阳的物理课》探讨太阳光压( 三 ) 本文转自：北青网光竟然具有

其中已经代入dΩ的公式。将这个结果除以(dr)^3就得到微元dS提供在球心处的能量密度：

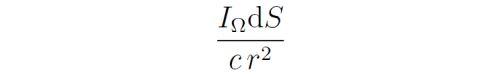
文章图片

文章图片

对这个结果沿着整个球面积分就得到球心的能量密度：

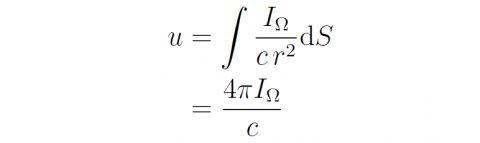
文章图片

文章图片

或者等价地有I_Ω=uc/(4π) 。紧接着，再推导u和I的关系。根据定义有：

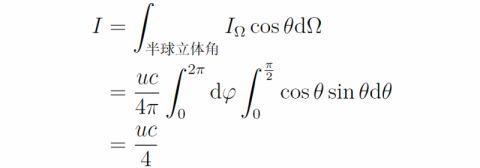
文章图片

文章图片

其中已经代入I_Ω=uc/(4π)用以化简。接下来，开始推导辐射对黑体表面的压强。当系统达到平衡时，黑体吸收多少辐射就会发射多少辐射，因此可以等效为辐射照射到黑体表面后被完全反射出来。另一方面，不同频率的光子其能量和动量是不一样的，因此需要单独考虑每个频率，从而要把I_Ω看成关于频率的积分：

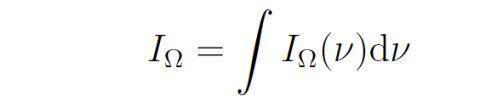
文章图片

文章图片

张朝阳表示，对于以θ角入射的频率为ν的光，除以光子能量hν就可以算出入射光子数，由于每个光子动量为hν/c ，考虑角度θ导致的投影，就可以得到单位时间单位面积上以立体角dΩ入射的dν频段的光子所传递的动量：

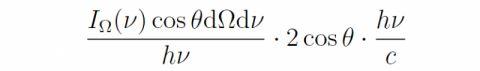
文章图片

文章图片

其中因子2是考虑了反射，即动量改变要乘以2 。单位时间的动量改变就等于力，再加上考虑的是单位面积，因此上式就是这部分光对黑体的压强。注意上式的两处hν刚好消掉，因此对整个频段的积分其实就只是对I_Ω(ν)的积分，对I_Ω(ν)的整个频段积分结果是I_Ω 。再对整个半球立体角积分就可以得到总压强：

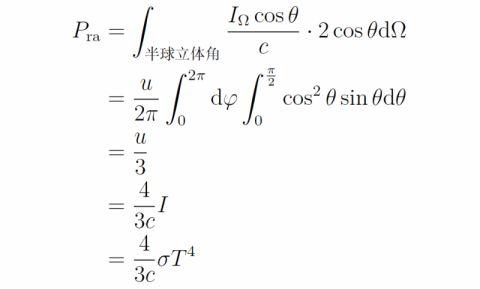
文章图片

文章图片

下图就是张朝阳在直播课上推导出的黑体辐射压强与温度的关系式：

文章图片

文章图片

张朝阳推导黑体辐射压强公式
接着，他将刚刚得到的黑体辐射压强公式应用到计算太阳辐射层光压的场景中。张朝阳打趣道，现在气体压强的“援军”到了，我们还需要知道这个“援军”能不能抵抗住引力的压缩。因为太阳中心温度是一千多万开尔文，而温度随着半径的下降是相对缓慢的，因此张朝阳假设辐射层温度为700万开尔文，将其代入光压公式，得到光压约为10^12 Pa量级(注：具体代入相关数据后得到的值约为6×10^11 Pa) 。
他指出，前面估算得到太阳中心压强是1.7×10^16 Pa ，如果辐射层某处密度是核心层平均密度的千分之一，那么根据前面的推导，辐射层这一处的压强就是1.7×10^13 Pa 。假如温度的缓慢下降使得气体压强不足以提供所需的1.7×10^13 Pa ，根据刚刚推导的光压量级，光子是有望提供相应的压强作为补充的。
持续打造知识直播平台搜狐视频吸引诸多科普播主入驻
截至目前，《张朝阳的物理课》已直播四十余期。从去年11月开启第一节物理直播课，他先是从经典物理学开始，科普了牛顿运动定律等；而后从经典物理的“两朵乌云”说起，向近现代物理过渡，探讨了黑体辐射理论中的维恩公式、普朗克公式等知识。此后逐步进入量子力学领域，从基础的薛定谔方程等理论内容，到氢原子波函数，再到气体定容比热的温度阶梯等更加具体实用的案例。内容丰富、覆盖广泛，理论公式由浅入深、繁简交融。