MM宇宙，唯一被证实的广义相对论混沌解，是理解量子引力的关键( 二 ) 我第一次接触混沌理论是通过

虽然混沌是一个很容易理解的概念，但它是出了名的难以证明。我们所知的大多数混沌系统都是一维或二维的，证明多维系统混沌的标准方法实际上是将其简化为一维问题。因此，证明一个四维宇宙学是混沌的是一个艰巨的任务。
但首先，混沌（ chaos）与混合有（mixing）什么关系？
在19世纪，科学家们试图了解物质如何混合的数学原理，在什么条件下可以认为是混合，以及什么过程导致混合。他们发现了四个层次的混合：遍历混合（ergodic）、弱混合（weakly mixed）、强混合（strongly mixed）和伯努利移位（Bernoulli shifted）。
假设你正在制作鸡尾酒，有10%的朗姆酒和90%的可乐。你可以制作一种混合方式的鸡尾酒。
遍历混合的鸡尾酒是混合得最不均匀的，如果你取任意体积的朗姆酒和可乐，随着时间的推移，朗姆酒的平均含量是10% 。这意味着在任何特定时间朗姆酒的比例可能是任何值。
对于混合程度较弱的鸡尾酒来说，除了偶尔有一次，体积中有10%的朗姆酒。
对于烈混合的鸡尾酒，朗姆酒的比例始终是10% 。
伯努利移位的鸡尾酒不仅总是10%的朗姆酒，而且鸡尾酒的“结构”在每一时刻都是完全随机的，你可以把它看作是一种不仅混合良好，而且处于不断搅拌状态的鸡尾酒。
伯努利移位混合也被称为phi-混合，是一种特殊的混合，因为它是伪随机的。它可以用于伪随机数生成器，并可能是布朗运动的原因。许多混沌系统表现出这种混合，包括Mixmaster宇宙。

文章图片

文章图片
让我们看一些混沌系统的例子。
理解混沌系统的最简单方法是使用所谓的映射，这只是系统状态x在时间n和时间n+1之间的关系。如果它是一个一维系统，那么x只是一个数字。
逻辑斯谛映射（The logistic map）是最古老的混沌映射之一，模拟人口的增长和崩溃。逻辑斯谛映射并不总是混沌的。相反，它可能是也可能不是，取决于一个可控参数的大小。

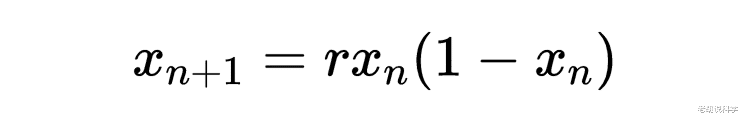
文章图片

文章图片
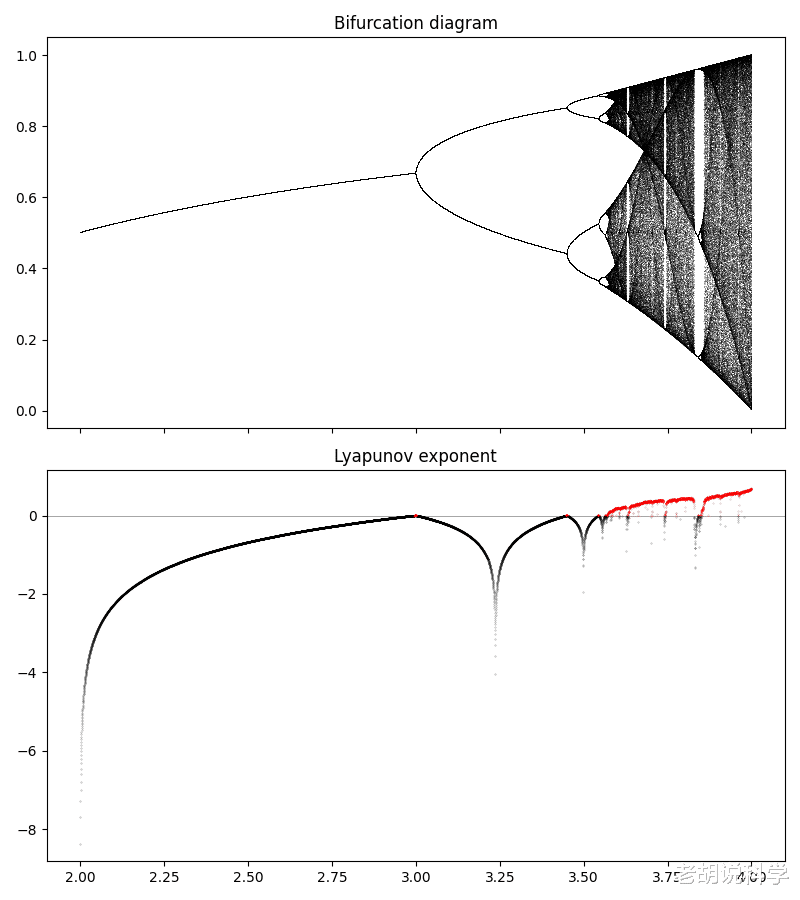
这里的可控参数是r ，唯一能控制的是它的起始位置。如果让这个映射运行一段时间（用一点Python代码就可以轻松搞定），它将趋向于收敛到一个或两个或更多的点，或者完全随机。你可以把所有这些收敛点收集到一个叫做分叉图的图中。我通过对10000个r值的地图进行1000次迭代，并对每个r值的最后100次迭代进行绘制，创建了一个分叉图。

文章图片

文章图片
你可以通过看图知道它在哪里变得混沌。这100个值在图上到处都是。但用数学的方法来看，就是计算李亚普诺夫指数，这是衡量其相空间中两个相邻轨迹发散的速度。如果这个指数是负的或者是零，这意味着系统收敛到一个特定的状态叫做不动点或者变成周期性的，那它就不是混沌的。如果它是正的，它就是混沌的。
这里的一个有趣的特点是，你可以看到在走向混沌的过程中，状态会经历一个叫做 "周期加倍 "的东西。一开始是小的r ，小于3 ，收敛到一个单一的固定点。在那之后，它在两个状态之间徘徊。然后它再次翻倍到4 。每次翻倍，李亚普诺夫指数都达到零，与混沌接近，然后在上升之前再次下降。你看不出来，但周期继续翻倍2、4、8、16、32 ，但是在r的范围内，它们每一周期花费的时间变短了。然后你可以看到，在r=3.57左右，它变得混沌。仍有一些短暂的时期，它又回到了非混沌状态。你可以在随机性之间看到那些白条。