另一个例子是切比雪夫多项式（ Chebyshev polynomials） 。有无数个这样的例子 ， 它们都具有很强的混沌性 。
这里是一个三阶切比雪夫：

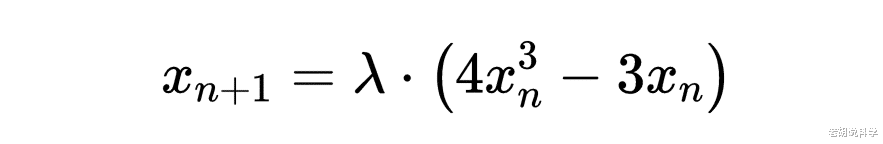
文章图片

文章图片
这些地图很混沌 ， 它们可以代替完全随机的噪音 。

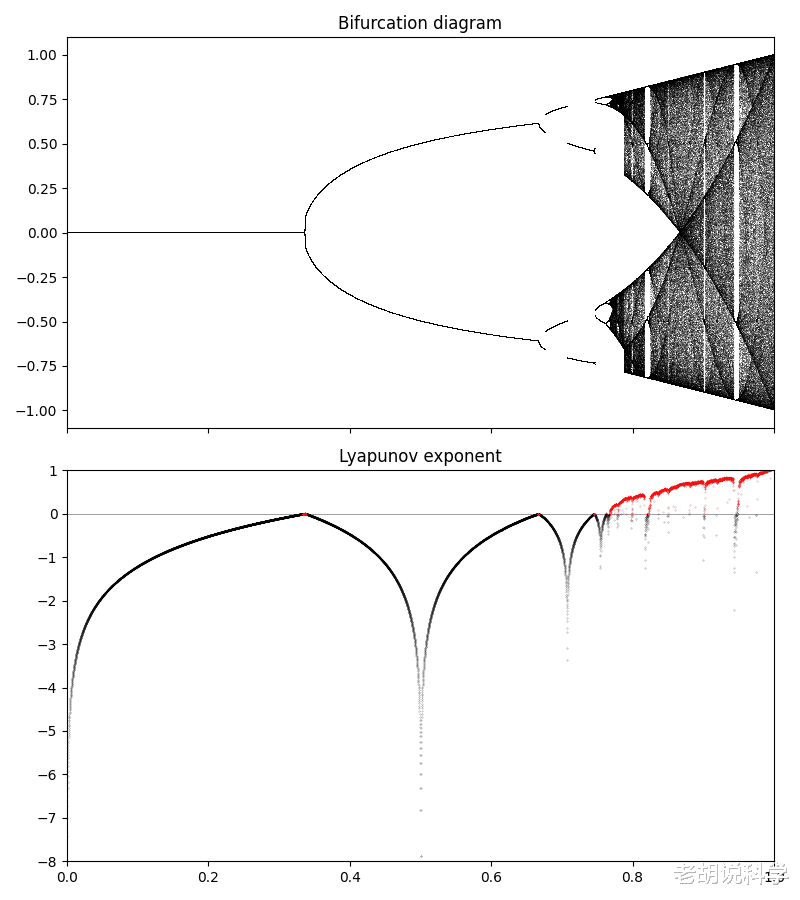
文章图片

文章图片
切比雪夫多项式也被用于密码学中 ， 因为它们不可预测 ， 但对0非常对称 。
现在 ， 让我们来谈谈Mixmaster宇宙中的混沌情况 。
Mixmaster引入了三个比例因子 ， a、b和c ， 每个空间方向都有一个 。因为它们是同质的 ， 所以它们随时间变化 ， 但不随空间变化 。另一方面 ， 因为它们都可以是不同的值 ， 所以宇宙不是各向同性的 。
你可以将下面的Mixmaster宇宙与标准宇宙 ， 即FLRW宇宙进行比较 ， 后者只有三个方向的一个比例因子 。

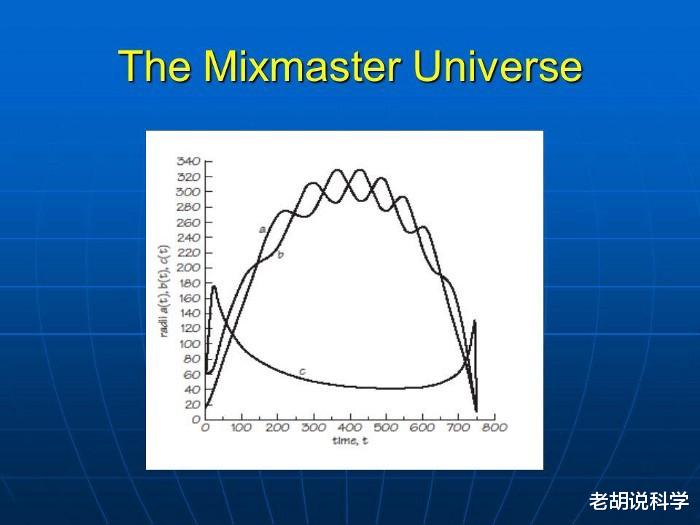
文章图片

文章图片
两个比例因子振荡 ， 而一个收缩和膨胀 。(约翰-D-巴罗)

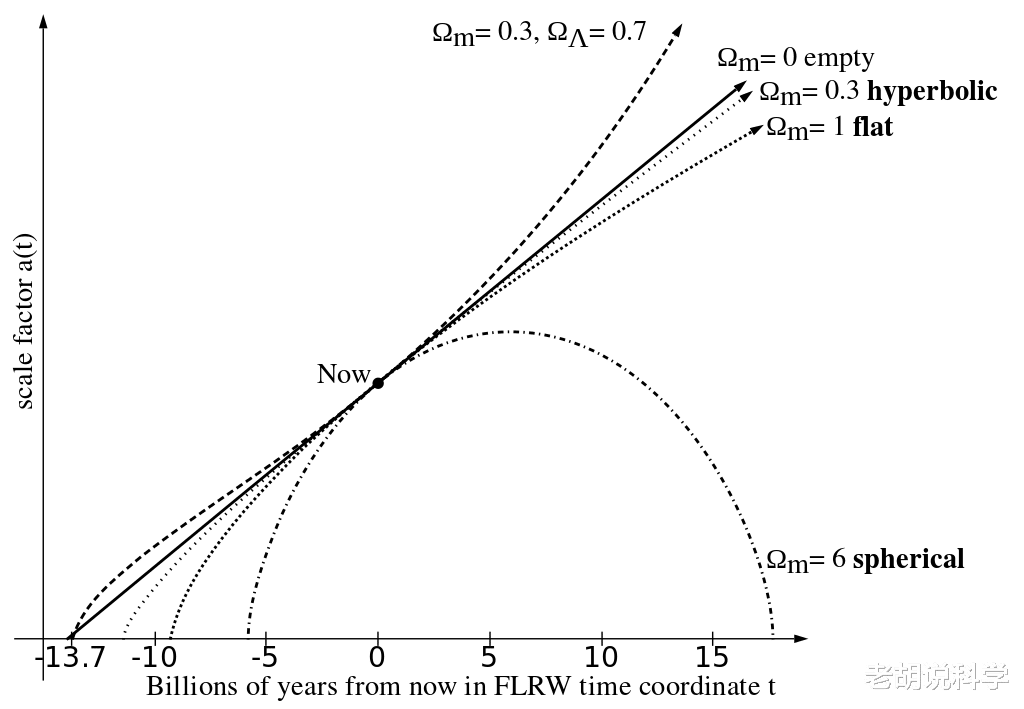
文章图片

文章图片
FLRW宇宙学（维基媒体）
为了证明Mixmaster宇宙是混沌的 ， 你必须把它还原成一个一维映射 。爱因斯坦方程保证了其中一个比例因子 ， 比如说c ， 取决于另外两个 ， a和b ， 所以它已经是二维的了 。
在这种情况下 ， 两个维度仍然太多 ， 我们可以使用一个数学技巧将其进一步减少到一个维度 ， 这个数学技巧被称为庞加莱回归映射 。一些二维或更多维的空间 ， 那么你该空间的轨迹必须通过它的一个横截面 。
如果回归映射是混沌的 ， 那么高维一定也是混沌的 。我们可以证明 ， 该映射对于Mixmaster是混沌的 。

文章图片

文章图片
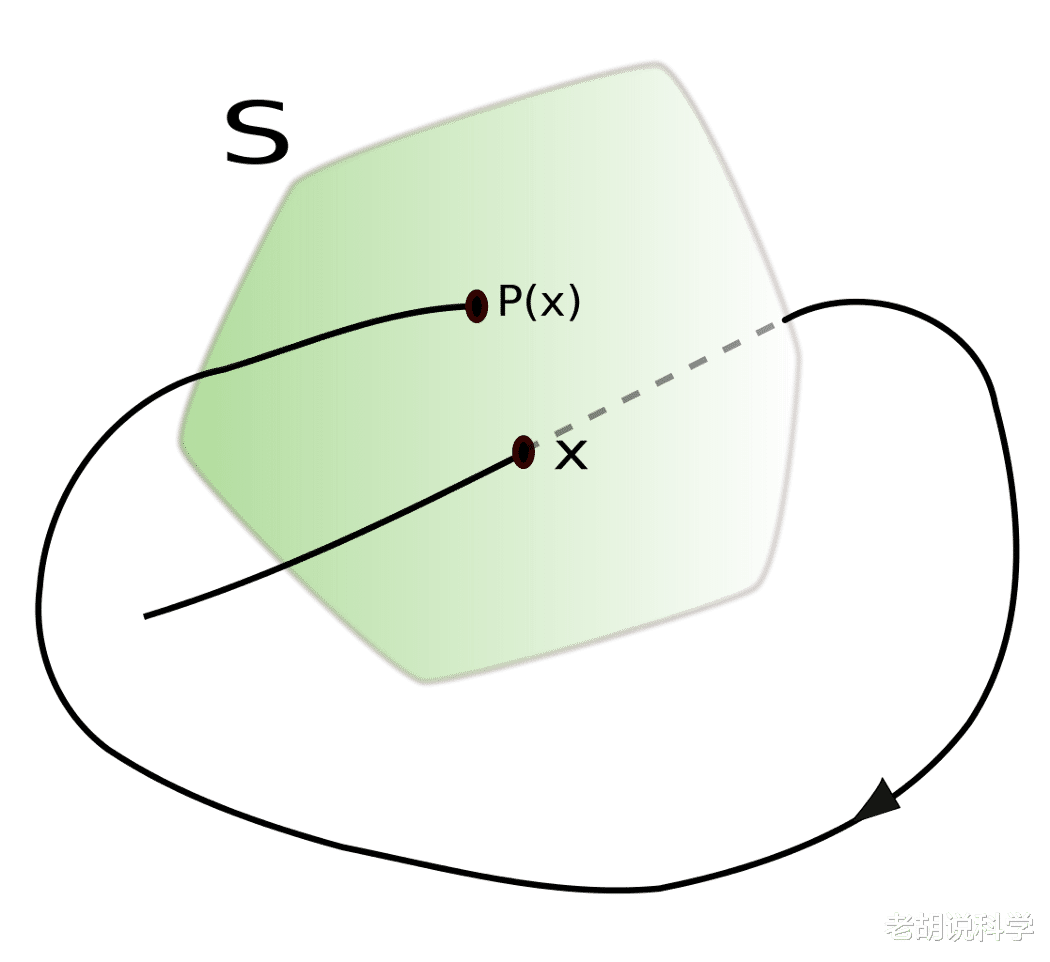
庞加莱地图 。
不幸的是 ， 在爱因斯坦的宇宙中 ， 这还不够 ， 因为我们总是可以选择新的坐标系 ， 我们怎么能知道没有一个坐标系可以完全消除混沌的呢？尤其是李亚普诺夫指数 ， 是依赖于坐标的 ， 所以在这种情况下作为混沌的指标是不可靠的 。
在90年代末 ， 人们设计了一种与坐标无关的分形方法 ， 并表明米斯纳的宇宙确实是混沌的 。
这种分形方法（而不是研究对初始条件的敏感依赖） ， 表明Mixmaster宇宙的动力学包含一个奇怪的排斥物 ， 它类似于一个奇怪的吸引子 ， 但具有排斥性 ， 因为系统倾向于远离它而不是流向它 。这有点像球滚向山顶而不是山谷 。
趋向于被一个特定的吸引子吸引或被一个排斥子排斥的一组初始条件被称为它的吸引盆地或排斥盆地 。如果该盆地有一个边界是分形的 ， 那么你就知道它是一个奇怪的吸引子或排斥子 ， 系统是混沌的 。
例如 ， 二维系统：

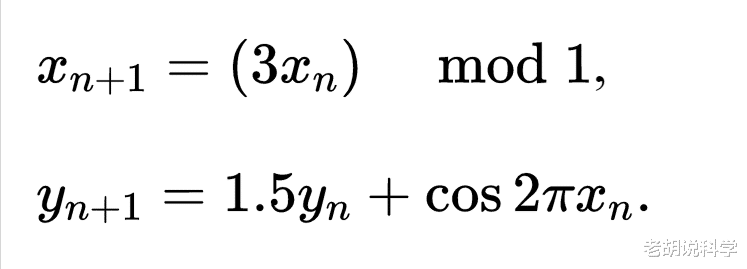
文章图片

文章图片
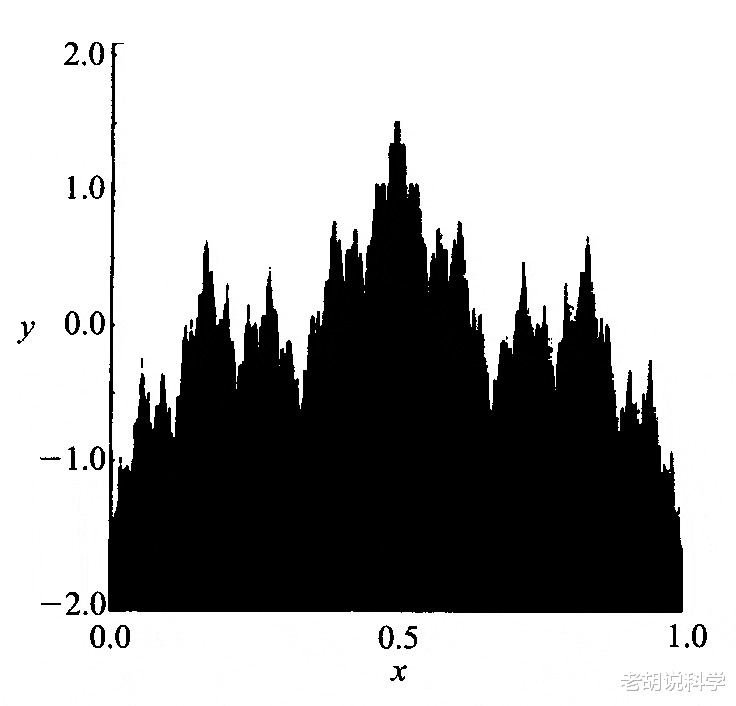
有一个分形盆地边界 ， 你可以在所有的峰上看到：

文章图片

文章图片
Mixmaster宇宙有一个类似的分形边界 。对于数学来说 ， 当膨胀理论作为CMB的一个良好的解释时 ， 所有对Mixmaster宇宙的兴趣都消失了 。但我认为 ， Mixmaster宇宙还是值得研究的 。

• 海尔冰箱爱的新鲜式｜被“嫌弃”的老妈
• 微软、动视暴雪并购电话会实录：元宇宙、云游戏，开启新一轮全球硬科技战事
• 梦幻新诛仙被动法宝选哪个（梦幻新诛仙被动法宝最强选择建议）
• 被李想质疑“刷新了创业者的底线” 团车CEO闻伟回应
• 和数研究院被授予首批苏州工业园区“区块链重点企业”
• 利用哈勃望远镜，我们能够看到130多亿年前的宇宙
• 蚂蚁新村|蚂蚁新村1月19日答案最新（被誉为中国玉雕第一镇的是）
• 为了3万工人的利益，他被砍7刀，流尽最后一滴血
• 光遇一个朋友赞了你的留言什么意思（光遇被赞留言情况解析）
• 三星电子在芯片投资领域首次被台积电超越