凝聚态物理学的新篇章——超越朗道范式的拓扑量子物态( 三 ) 在凝聚态物理学发展历程中

02
超越朗道范式的拓扑量子物态
以二维量子霍尔效应为范例，我们简要回顾拓扑物相的发展，试图勾勒出弱相互作用系统中拓扑电子态的基本物理。在固体材料中，弱相互作用的电子由于量子效应而形成分立的能带结构，从而可以形成绝缘相。在绝缘相中，电子激发态需要克服有限能量，因而在低能下没有电子激发，似乎与真空无异。然而，自从20世纪80年代发现量子霍尔效应以来，人们发现在绝缘体中有一大类特殊的绝缘体，尽管其块体内无低能的电子激发，但是在其边缘上却有不需要克服能量的无能隙激发态，并且还具有强的鲁棒性，其背后的根源正是拓扑相位因子。
2.1 量子霍尔效应
在磁场中，二维电子气会受到洛伦兹力而围绕磁通发生回旋运动，在能谱上形成朗道能级，其能级间距正比于回旋频率，取决于磁场大小和电子有效质量。每个能级具有与体系尺寸相匹配的巨大简并度，因为在实空间上每个量子磁通就对应于一个电子轨道。由于泡利不相容原理，当电子填满整数个能级的时候，再增加一个电子需要克服系统能隙，所以该体系为“不可压缩”绝缘态。尽管体内激发具有能隙，但在实验上观测到量子化的横向电导表明其系统边缘存在稳健的单向流动的无能隙电子态模式，这就是量子霍尔效应。横向电导的量子化暗示了其内在的拓扑性。在1982年， Thouless ， Kohmoto ， Nightingale与denNijs四人首次提出了TKNN公式来刻画量子霍尔态的拓扑本质，并且将其体块和边缘的横向电导联系了起来[8] 。TKNN公式本质上就是从集体激发的电子波函数中提取出Berry相位。
要理解Berry相位通量的量子化，一个最简单而又具有代表性的例子就是考虑一个连续动量空间中的狄拉克(Dirac)旋量波函数，粒子受到磁单极子的作用：

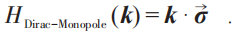
文章图片

文章图片
其对应的基态本征波函数为

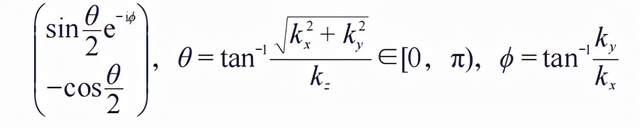
文章图片

文章图片
其中θ ，为球面角参数。然后，我们可以求得Berry联络：

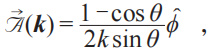
文章图片

文章图片
以及在不同纬度圆轨迹上的Berry相位：

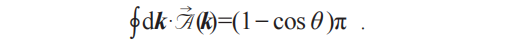
文章图片

文章图片
当θ=0 ，也就是环绕北极点的无穷小轨迹其获得相位为0；当θ=π/2 ，其获得π相位；而当θ=π ，将获得2π相位。也就是说，磁单极子具有2π的量子化的Berry通量。确实，狄拉克磁单极子携带着一根具有2π Berry通量的狄拉克弦。在我们这个例子中，该弦从奇点向南极无穷延伸，如图2所示。此外，狄拉克磁单极子Berry通量的量子化与二维空间中的Berry通量的量子化密切相关。只要我们取一个映射：

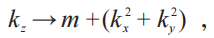
文章图片

文章图片
其中m代表狄拉克费米子的静质量。如此定义了从二维空间到三维空间的一个曲面映射，直观上相当于将二维动量平面嵌入到三维空间中，或者说把三维中的一个曲面摊开延展到二维平面(图2) 。简单分析看到，当m0则对应于0通量。通过这个简单而又具有代表性的例子，我们可以窥见，二维封闭流形中的Berry通量量子化本质上是因为三维空间中磁单极子的量子化，对应于二维空间中的一个拓扑结构，称为斯格明子(skyrmion) 。