凝聚态物理学的新篇章——超越朗道范式的拓扑量子物态(11) 在凝聚态物理学发展历程中

从拓扑序的角度看，希格斯相变和电荷禁闭相变分别对应于任意子e与m的凝聚，可作为拓扑序之间相变的任意子凝聚机制的一个典范[32] 。目前，已知的任意子凝聚主要指的还是具有玻色型自统计的任意子发生凝聚，比如这里的电荷与磁荷。它与常规的玻色凝聚的区别在于，这类玻色子与其他任意子之间由于Aharonov—Bohm相位效应存在非平庸的统计，从而其凝聚会引发其他任意子的禁闭。在Toric Code模型中，由于磁荷m对电荷e来说充当着π通量的角色，所以磁荷的凝聚会导致电荷的禁闭。直观的图像理解是，在磁荷凝聚的基态真空上，磁荷可以任意涨落出现或者消失，而这意味着电荷在真空中游走时会感受到涨落的相位，从而造成干涉相消效应。从逻辑上说，由于电荷在磁荷凝聚的真空中已经不具备良好定义的统计相位，所以不允许独立存在。同理，电荷的凝聚会导致磁荷的禁闭。
由电磁对偶相联系的希格斯相与禁闭相，在相图上被Fradkin和Shenker论证可以绝热连接。早在1980年， Jongeward等人通过数值计算发现希格斯相与禁闭相之间的电磁对偶线上，在弱场下出现一级相变线[33] ，起始于一个临界点，终结于Z2退禁闭相的边缘，与希格斯相变线和禁闭相变线交汇在一起，疑似出现一个三相变点。30多年以后，在Toric Code模型提出以后，人们从磁场扰动的角度，以探索拓扑相变为动机又对类似相图进行了大量探索。一个重要的工作是，在2010年， Tupitsyn ， Kitaev ， Prokof′ev与Stamp通过将该模型映射到三维经典伊辛模型，并使用大规模蒙特卡罗数值计算的办法再一次计算了此相图[34] 。然而，其数据仍然无法敲定在疑似三相变点的区域上的情况，如图9(a)所示。其中最让人感兴趣的是三相变点的可能，尽管这样的三相变点超越现有的任意子凝聚机制。因为在电磁对偶路径上，从拓扑相出发，如果发生电荷凝聚，则电磁对偶意味着磁荷也同时发生凝聚。然而由于常规的宏观凝聚体是玻色性的，所以Aharonov—Bohm效应会阻止电荷凝聚体与磁荷凝聚体的共存。也就是说，狭义的任意子相变机制无法解释三相变点。因此，尽管围绕该相图已经有了可观的理论与数值的研究，然而在电磁对偶线上的疑似三相变点依旧是未解之谜。自对偶线上的一级相变线和来自希格斯相变与禁闭相变的连续相变线是如何交接？假如是连续的三相变点，那么从拓扑相到非拓扑相的相变机制是什么？任意子命运如何？

文章图片

文章图片
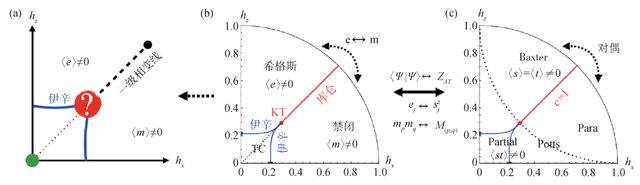
图9 (a)扰动Toric Code模型的全局相图示意。绿点标记无微扰的Toric Code模型的Z2规范退禁闭拓扑相，蓝线标记三维伊辛类的拓扑相变，包括电荷凝聚的希格斯相变和电荷禁闭/磁荷凝聚相变。当电磁对偶时，电荷凝聚相与磁荷凝聚相之间出现一级相变线，它起始于一个临界点上，类似于气液相变，终结于拓扑相边界；(b)从拓扑量子态多体波函数获得的相图；(c)拓扑量子态多体波函数所对应的经典Ashkin—Teller统计模型的相图
2019年初，本文作者另辟蹊径，从严格可调节的基态多体波函数的角度，探究了沿着电磁对偶路径上的可能发生的拓扑相变[35] 。这类似于Laughlin写下的刻画分数量子霍尔态的多体波函数[18] ，只不过我们将其思路推广到含参数调节的波函数来刻画一个拓扑量子相变的过程。同样，类似于Laughlin可将其多体波函数的模方映射到二维经典库仑等离子体问题论述分数霍尔态的性质，我们发现含参数调节的ToricCode波函数的模方也可以映射到经典Ashkin—Teller统计模型。为此，我们借助于张量网络态表象，因为张量网络态可以把一个多体波函数分解为一个个局域的张量的直乘积形式[35] ，而局域的张量结构描述的则是物理自由度与某种“纠缠自由度”的耦合。