凝聚态物理学的新篇章——超越朗道范式的拓扑量子物态( 八 ) 在凝聚态物理学发展历程中

然而，基于高温超导体系的RVB是由长程的自旋单态组成，其自旋子无能隙而具有费米面，研究起来非常复杂。为此， Rokhsar与Kivelson提出了量子二聚态模型[24] ，考虑更原始的短程RVB态中的拓扑激发，用简化的二聚化构型来刻画短程RVB的极限，即退禁闭的自旋子以及演生涡旋规范场，如图5所示。而文小刚则从隶玻色子(slave boson)分解与演生规范场的角度提出了该体系中的Z2拓扑序的概念[25] 。随后， Moessner与Sondhi从数值计算上验证了该系统所具有的Z2拓扑序[26] 。然而，真正彻底的征服来自1997年Kitaev在arXiv上发布文章所提出的严格可解模型，该模型简单且严格可解，展现出相应的克服能隙的任意子激发与基态拓扑简并[27] 。
3.3 Z2自旋液体态
1997年， A. Kitaev在arXiv上发布一篇名为《藉由任意子实现可容错的量子计算》的文章，首次提出一个名叫Toric Code的自旋模型，名字取义于在圆环面上作量子编码，文章后来正式发表于2003年。该自旋模型严格可解，其基态为量子自旋液体，可以完美地展示Z2内禀拓扑序。该模型十分简约，只保留了最核心的拓扑的信息。与RVB自旋液体不同，此模型并不具有自旋旋转不变性，从而充分展示了Z2量子自旋液体的本质不在于对称性。出于这个模型的极简性与严格可解性，以及Z2内禀拓扑序的基础性，该模型在拓扑序研究领域中的地位堪比伊辛模型在相变研究中的地位，是许多理论和实验研究的一个试金石。
Toric Code模型最初定义在一个周期边界条件的正方晶格上，自旋1/2物理自由度处于格点连边上，其哈密顿量表示为

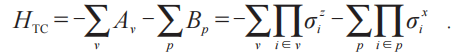
文章图片

文章图片
其中顶点Aj算符与元格Bp算符分别定义在顶点与元格(plaquette)上，如图6(a)所示。四自旋相互作用项表面上十分复杂，但是每一个局域的Aj或者Bp都是守恒量，这是由于自旋1/2的泡利算符反对易，而顶点算符和元格算符之间总有偶数自旋交叠，从而抵消了负号。因此，任意的本征态都可以由所有的局域算符的本征值来完全确定，模型严格可解。

文章图片

文章图片
图6 (a)Toric Code 模型中四个自旋乘积形成的相互作用项；(b)Toric Code 模型的基态可以表示为所有闭弦等权相干叠加形成的弦网凝聚态
当我们将自旋朝上视作参考真空，而自旋朝下看作弦的一段，那么Toric Code模型的基态可以表示为包含所有闭弦等权重相干叠加态，如图6(b)所示。这种闭弦凝聚态可以看成是传统玻色子凝聚态从点粒子推广到弦这样的延展对象，并且闭弦在基态中可以任意涨落不耗散能量。其实，在经典伊辛统计模型中，高温极限下自旋无序涨落，磁畴壁发生任意的热涨落。如果把闭合畴壁当作基本自由度，该热力学系统则为发生热涨落的各种畴壁。这样的伊辛统计模型与Toric Code模型的基态有着深刻的内在联系。
实际上， Toric Code模型等价于一个描述二维空间中最简单的离散化的电磁场理论，其低能激发包含的准粒子有：电荷e、磁通m、马约拉纳费米子f 。由于不同格点的σx之间相互对易，所以m粒子相互缠绕的轨迹算符可以等价于一串m闭弦算符作用到基态波函数上，并不出现任何相位，从而m粒子之间具有玻色统计。同理，不同的e粒子相互之间缠绕也不产生相位而同样具有玻色统计。然而，关键的是当一个e粒子环绕一个m粒子一周缠绕时，其运动轨迹涉及一条e弦与一条m弦的相交。由于 σxσz = -σzσx ，从而它们之间的交换会贡献一个“-1” ，即导致π的Berry相位，如图7所示。也就是说，尽管各自满足玻色子统计，但是e与m粒子相互间却具有非平庸的统计相位π ，人称“semion统计” 。如此一来，可以简单验证， e粒子与m粒子的复合粒子具有费米统计，记为 f = em 。从一个纯粹的玻色自由度的微观模型中，竟然演生出了费米子激发，这不可不谓神奇！如此，我们便确立了该体系中的三种基本低能拓扑激发准粒子e ， m ， f 。广义上说，它们都属于任意子。