凝聚态物理学的新篇章——超越朗道范式的拓扑量子物态( 九 ) 在凝聚态物理学发展历程中

文章图片

文章图片
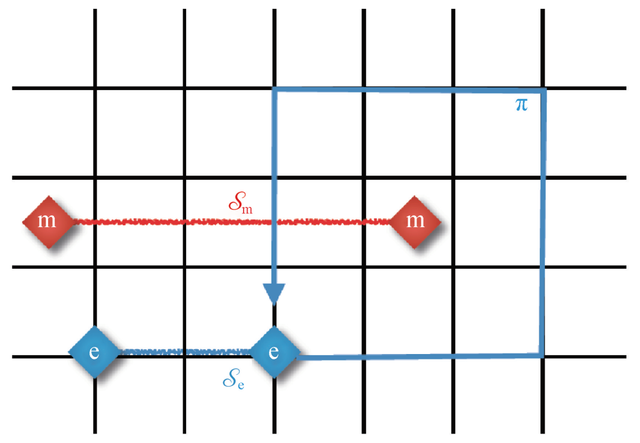
图7 弦算符激发的拓扑粒子及其统计关系。蓝色粗线代表电荷e弦，红色粗线代表磁通m弦，其各自末端为拓扑准粒子。可以验证电荷e弦环绕磁通m弦一圈后，发生Aharonov—Bohm效应导致π相位
每一种任意子激发都具有拓扑稳定性，不同的任意子类型只能通过融合来转变，比如e型任意子只能通过与f型任意子融合来得到m型任意子。一般而言，任意子的融合遵循一个简单而基本的代数原则。Toric Code模型任意子的融合原则是

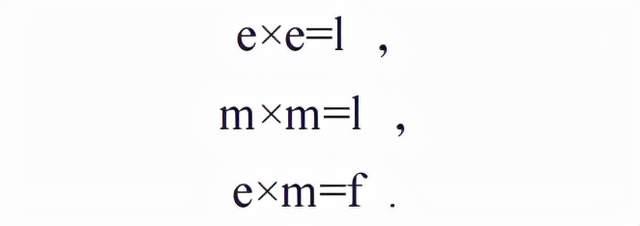
文章图片

文章图片
事实上这组融合规则连同任意子的统计定义了一种拓扑序。在三角晶格短程RVB自旋液体中，虽然微观晶格不同，对称性也不一样，但是其中的基本拓扑激发却遵循同样的统计和融合规则，即费米型的自旋子围绕着玻色型的演生规范场vison(π通量涡旋)转一圈会产生π通量激发。所以，三角晶格上的短程RVB自旋液体与Toric Code模型同为一个普适类，称为Z2拓扑有序。之所以称作Z2 ，是因为其低能激发演生出了Z2规范场。
尽管Toric Code模型是在离散的正方晶格上通过自旋模型定义的，但是其封闭弦凝聚的基态图像具有长波极限的特质，因而可以推广到任意的微观晶格。一般性而言，可以完全脱离晶格而通过定义一组连续化的弦构型来构造属于同一个普适类的Z2内禀拓扑序。除此之外，通过定义更丰富代数结构的弦构型，还可以得到更加广泛的弦网凝聚拓扑态。由于弦的非局域特质，这些模型都具有自带拓扑稳定的任意子激发，即内禀拓扑序。事实上， Michael Levin与文小刚在2005年的工作中展示，弦网凝聚图像可以演生出所有的二维非手征的拓扑序[28] 。因而，弦网凝聚是一个强有力的物理图像，它从某个角度简明直观地概括了非手征拓扑序的本质属性。
事实上，由于基态的局域特征已经被稳定子算符锁死，即局域上不存在开放的e弦或者m弦，所以如果将体系放在一个球面上，则只有唯一基态。尽管很难想象如何将正方晶格放置在球面上，但是闭弦凝聚却可以置于连续空间中，所以可以放置在球面上乃至更一般的拓扑流形上。然而，对于两个方向都为周期性边界条件的正方晶格，相当于将闭弦凝聚体放置在一个圆环面上，这时候环绕两个不可收缩大圆的全局闭弦数目的奇偶性将导致出现四个正交的简并基态。由于局部涨落只能产生可收缩的局部闭弦，全局闭弦可以发生形变或者成对涨落，但是其数目的奇偶性不会改变，因而是一个稳定的全局量子数。不同的基态可以用全局弦算符来转换，也可以用对偶的横向全局弦算符来探测。具体而言，我们可以定义环向 (x方向) 和极向 (y方向) 不可收缩的全局e弦和m弦算符，如图8所示，可以验证除了相互垂直的全局e弦与全局m弦之外，其他的都相互对易。

文章图片

文章图片
图8 以两个方向的m弦数目奇偶性来区分的m弦表象的四重简并基态。其中裸的圆环面代表基态，带红圈的表示携带了全局弦算符。环向为x方向，而极向为y方向。对偶变换可以得到e弦表象下的四重简并基态
全局的弦算符作用到一个基态上使之变成另一个基态，这从物理图像上说其实就是产生一对任意子激发，并且使之围绕体系大环环游，其后再发生湮灭。由于四重简并基态之间只能通过全局的弦算符来联系，从而局域的微扰需要通过体系尺寸大小级别的巨大微扰才能将一个基态转换到另一个基态，导致两个基态在微扰下能级劈裂随着体系尺寸指数衰减。所以Toric Code模型的简并基态受到拓扑保护，这也正是为何Kitaev提出可以使用这类模型来编码量子信息，从而可以从物理层面上实现容错。